Вы можете изобразить линейное или квадратичное неравенство аналогично тому, как вы изобразили бы уравнение. Разница в том, что, поскольку неравенство показывает набор значений больше или меньше, ваш график будет показывать больше, чем просто точку на числовой прямой или линию на координатной плоскости. Используя алгебру и оценивая знак неравенства, вы можете определить, какие значения включены в решение неравенства.
Шаги
Метод 1 из 3: построение линейного неравенства на числовой прямой

Шаг 1. Найдите переменную
Чтобы решить неравенство, выделите переменную, используя те же алгебраические методы, которые вы использовали бы для решения уравнения. Помните, что когда вы умножаете или делите на отрицательное число, вам нужно перевернуть знак неравенства.
-
Например, если вы решаете неравенство 12 "> 12}"> 3y + 9> 12 { displaystyle 3y + 9> 12}
12"
12 "> 12}"> 3y + 9> 12 { displaystyle 3y + 9> 12}
12">
12-9 "> 12-9}"> 3y + 9−9> 12−9 { displaystyle 3y + 9-9> 12-9}
12-9
3 "> 3}"> 3y> 3 { displaystyle 3y> 3}
3">
{ frac {3} {3}} "> { frac {3} {3}}}"> 3y3> 33 { displaystyle { frac {3y} {3}}> { frac {3} {3 }}}
{ frac {3} {3}}
1 "> 1}"> y> 1 { displaystyle y> 1}
- В вашем неравенстве должна быть только одна переменная. Если ваше неравенство имеет две переменные, более целесообразно изобразить его на координатной плоскости, используя другой метод.
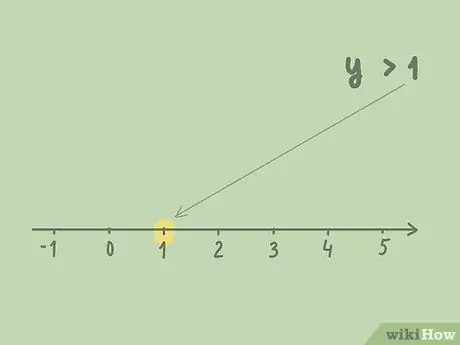
Шаг 2. Проведите числовую линию
Включите относительное значение в числовую строку (значение, которое, по вашему мнению, переменной меньше, больше или равно). Сделайте числовую строку максимально длинной или короткой.
-
Например, если вы обнаружили, что 1 "> 1}"> y> 1 { displaystyle y> 1}
1"
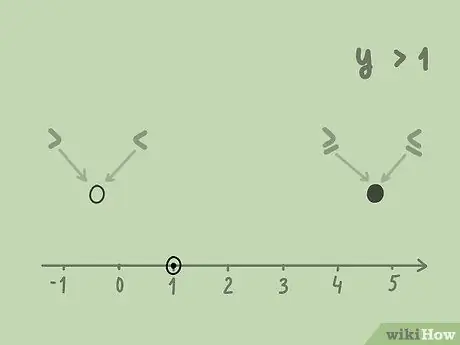
Шаг 3. Нарисуйте круг, обозначающий относительное значение
Если значение меньше (} ">> { displaystyle>}
">) это число, круг должен быть открытым, поскольку решение не включает значение. Если значение меньше или равно (≤ { displaystyle \ leq}
), or greater than or equal to (≥{displaystyle \geq }
), кружок должен быть закрашен, так как решение включает значение.
-
Например, для решения 1 "> 1}"> y> 1 { displaystyle y> 1}
1"
-
Например, если выполняется неравенство 3x-3 "> 3x-3}"> y> 3x − 3 { displaystyle y> 3x-3}
3x-3" y="3x−3{displaystyle"
. The y-intercept (the point where the line crosses the y axis) is -3, and the slope is 3, or 31{displaystyle {frac {3}{1}}}
. So, you would draw a point at (0, −3){displaystyle (0, -3)}
. The point above the y-intercept is (1, 0){displaystyle (1, 0)}
. The point below the y-intercept is (−1, −6){displaystyle (-1, -6)}
-
Например, для неравенства 3x-3 "> 3x-3}"> y> 3x − 3 { displaystyle y> 3x-3}
3x-3"
- For example, you might need to graph the inequality
-
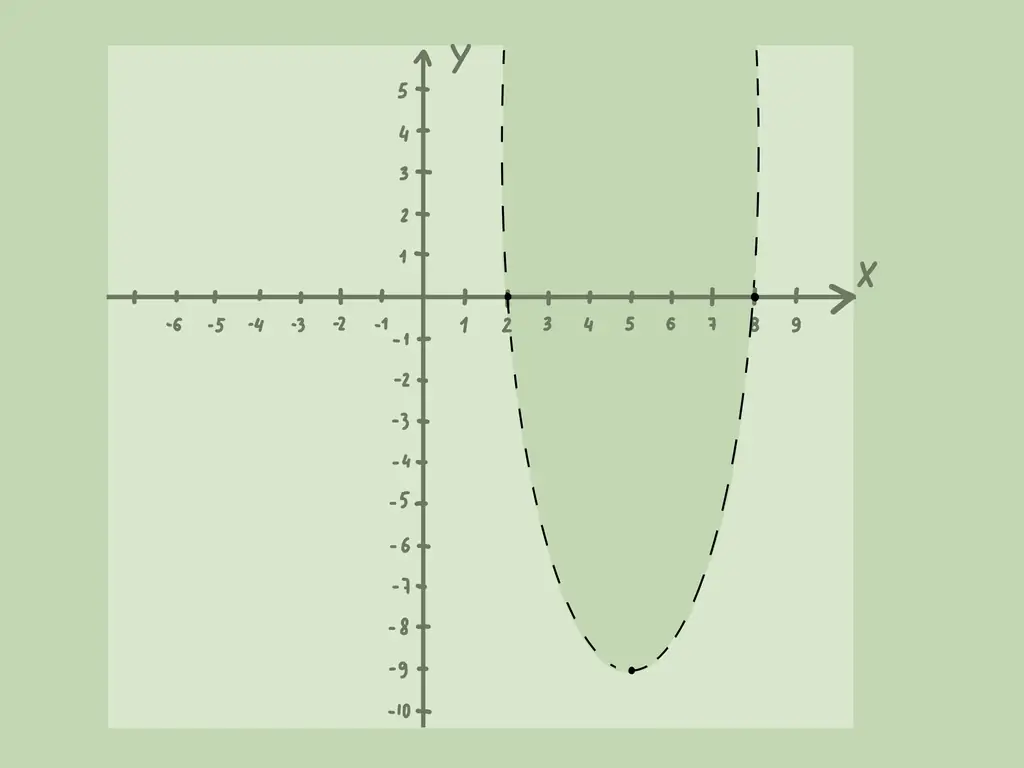
Например, за неравенство. Вершина находится в точке (5, −9) { displaystyle (5, -9)}
and the parabola crosses the x-axis at the points (2, 0){displaystyle (2, 0)}
and (8, 0){displaystyle (8, 0)}
- For example, for the inequality
-
For example, plugging the values of x{displaystyle x}
and y{displaystyle y}
of the point (0, 0){displaystyle (0, 0)}
into the original inequality, you get:
Since this is true, you would shade the area of the graph where the point (0, 0){displaystyle (0, 0)}
1"
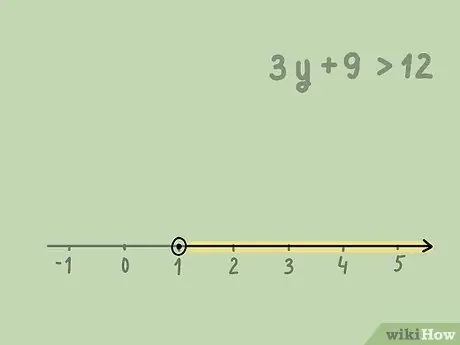
Шаг 4. Нарисуйте стрелку, указывающую включенные значения
Если переменная больше относительного значения, ваша стрелка должна указывать вправо, поскольку решение включает значения, превышающие это число. Если переменная меньше относительного значения, ваша стрелка должна указывать влево, поскольку решение включает значения меньше этого числа.
Метод 2 из 3: построение линейного неравенства на координатной плоскости

Шаг 1. Решите относительно y { displaystyle y}
You want to find the equation of the line, so to do this you need to isolate the y{displaystyle y}
variable on the left side of the equation using algebra. The right side of the equation should have the x{displaystyle x}
переменная и, скорее всего, константа.
9x"
9x "> 9x}"> 3y + 9> 9x { displaystyle 3y + 9> 9x}
9x
9x-9 "> 9x-9}"> 3y + 9−9> 9x − 9 { displaystyle 3y + 9-9> 9x-9}
9x-9">
9x-9 "> 9x-9}"> 3y> 9x − 9 { displaystyle 3y> 9x-9}
9x-9
{ frac {9x-9} {3}} "> { frac {9x-9} {3}}}"> 3y3> 9x − 93 { displaystyle { frac {3y} {3}}> { гидроразрыв {9x-9} {3}}}
{ frac {9x-9} {3}}">
3x-3 "> 3x-3}"> y> 3x − 3 { displaystyle y> 3x-3}
3x-3
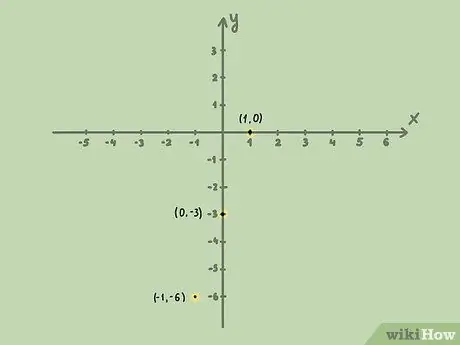
Шаг 2. Постройте линию на координатной плоскости
Для этого превратите неравенство в уравнение и нанесите график, как любое уравнение линии. Постройте точку пересечения оси Y, а затем используйте наклон для построения графика других точек на линии.
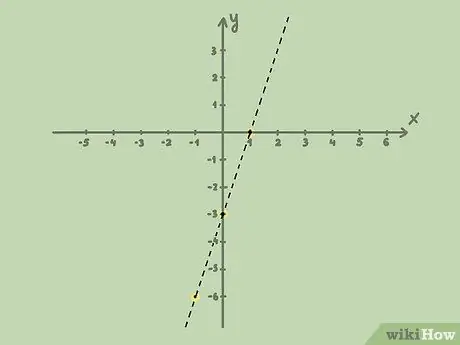
Шаг 3. Проведите линию
Если неравенство меньше (} ">> { displaystyle>}
">), линия должна быть пунктирной, так как решение не включает значения, равные этой линии. Если значение меньше или равно (≤ { displaystyle \ leq}
), or greater than or equal to (≥{displaystyle \geq }
) линия должна быть сплошной, поскольку решение включает значения, равные линии.
3x-3"
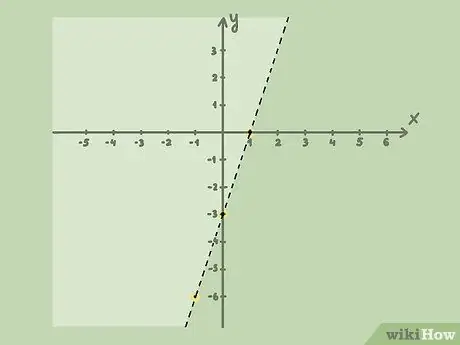
Шаг 4. Заштрихуйте соответствующий участок
Если неравенство показывает mx + b "> mx + b}"> y> mx + b { displaystyle y> mx + b}
Метод 3 из 3: построение квадратичного неравенства на координатной плоскости
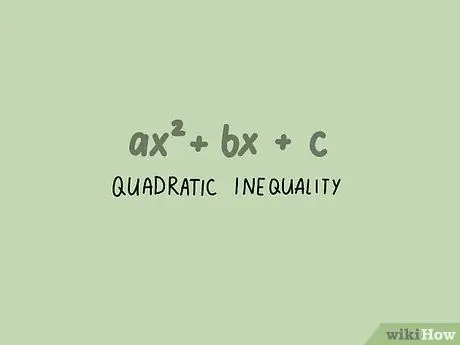
Шаг 1. Определите, есть ли у вас квадратное неравенство
Квадратичное неравенство принимает форму ax2 + bx + c { displaystyle ax ^ {2} + bx + c}.
. Sometimes there may not be an x{displaystyle x}
term or a constant, but there should always be an x2{displaystyle x^{2}}
term on one side of the inequality, and an isolated y{displaystyle y}
variable on the other side.
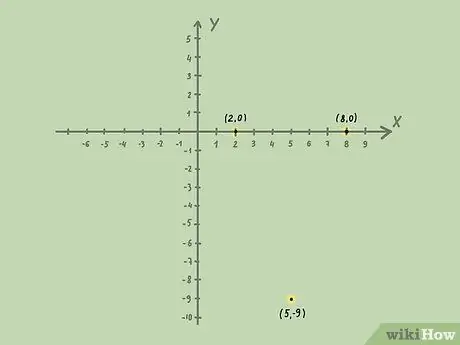
Шаг 2. Постройте линию на координатной плоскости
Для этого превратите неравенство в уравнение и нанесите линию на график, как обычно. Поскольку у вас есть квадратное уравнение, линия будет параболой.
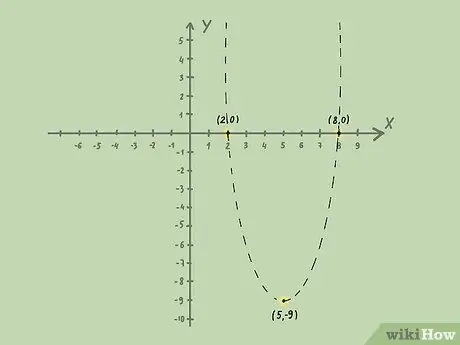
Шаг 3. Рисуем параболу
Нарисуйте параболу пунктирной линией, если неравенство меньше (} ">> { displaystyle>}
">). Если значение меньше или равно (≤ { displaystyle \ leq}
), or greater than or equal to (≥{displaystyle \geq }
), you should draw the parabola with a solid line, since the solution includes values equal to the line.
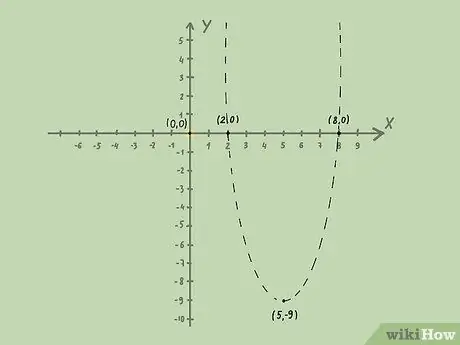
Шаг 4. Найдите несколько контрольных точек
Чтобы определить, какую область затенять, вам нужно выбрать точки внутри параболы и снаружи параболы.
Например, график неравенства находится вне параболы. Это было бы хорошим моментом для тестирования решения
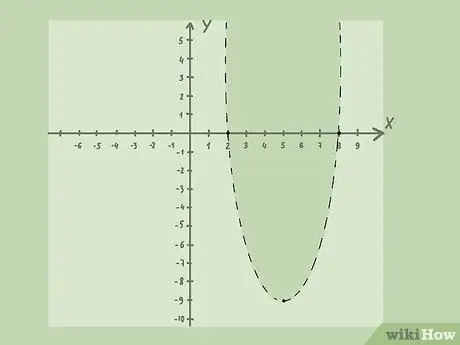
Шаг 5. Заштрихуйте соответствующий участок
Чтобы определить, какую область затенять, подставьте значения x { displaystyle x}
and y{displaystyle y}
from your test points into the original inequality. Whichever point produces a true inequality indicates which area of the graph should be shaded in.