Для Музея математики

Это заключительная часть нашей эпической серии Math Monday, посвященной сложному миру механических связей. См. введение в серию «Связи», где вы найдете MoMath Linkage Kit, введение и общие инструкции.
На протяжении всего сериала мы видели практические связи, такие как ножничный домкрат, пантограф или связь Уотта; и мы увидели невероятную универсальность даже четырехзвенной рычажной системы, которую можно заставить проходить через любые четыре желаемые точки. Мы также видели ограничения четырехзвенной рычажной системы - она никогда не может проследить идеально прямую линию. Но с помощью большего количества стержней и математической инверсии в круге это ограничение можно преодолеть, и с помощью многостержневых связей можно создать множество знакомых простых кривых. Вы также можете изучить гораздо больше о рычажных механизмах: рычажные механизмы, используемые в тяжелой технике, рычажные механизмы, встречающиеся в подвеске практически каждого автомобиля на дороге, парадоксальные рычажные механизмы, которые, кажется, вращаются с разной скоростью по или против часовой стрелки, трехмерные рычажные механизмы и многое другое.. Невозможно сделать такую серию исчерпывающей.
Итак, давайте завершим эту серию последним взглядом на разнообразие четырехзвенной рычажной системы. Вот один, не имеющий никакой практической цели - он просто создает причудливую кривую, напоминающую спирограф.
Связь Сангвина
Ингредиенты: Один батончик 40 (А); два 50-бара (Б и Д); один стержень на 60 с 30 отверстиями и ручка.
Направления: зафиксируйте букву A горизонтально. Свяжите A с B и C-0. Соедините C-60 с D и A. Вставьте ручку в C-30.
Использование: поверните B на полный оборот, удерживая ручку в отверстии, рисуя на бумаге. Обратите внимание, что полная кривая имеет две петли. Так что, возможно, вам придется снова пойти по кругу, заставив рычажок повернуть в другую сторону.
Вот изображение готового соединения:

И, наконец, вот связь Сангвина в действии, рисующая довольно красивую кривую, подобную гипоциклоиде:

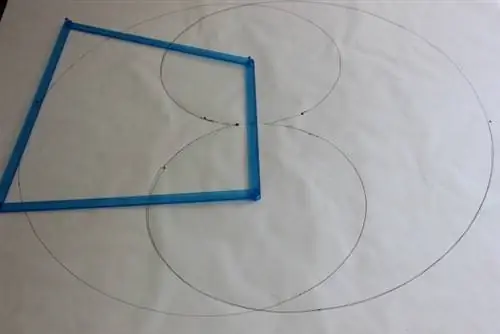
Напутственный вопрос: является ли какой-либо сегмент этой кривой дугой окружности? Почему или почему бы и нет?
Вот и все, что касается связей по понедельникам по математике, по крайней мере, на некоторое время. Надеюсь, вам понравился этот обзор связей так же, как мне понравилось его создание!
Final P. S.: Может ли человек, который зашел в MoMath на 26-й улице, 11 E и спросить о связях, отправить электронное письмо на адрес [email protected] со словом «связь» в теме? Спасибо!
- Связи, Введение
- Связи, часть 2: Четыре решетки, одна свобода
- Связи, Часть 3: Четыре стержня, две или три позиции
- Связи, Часть 4: Четыре такта, четыре позиции
- Связи, Часть 5: Четыре такта, больше позиций?
- Связи, часть 6: Биомимикрия
- Связи, Часть 7: Мир «Б. Х.»
- Связи, часть 8: В поисках прямолинейности
- Связи, часть 9: Давайте разберёмся
- Связи, Часть 10: Настоящий наркотик
- Связи, часть 11: Дайте им вторую степень
- Смотрите все наши рубрики «Математический понедельник»
